Lernhilfen
Mathe Lernhilfe
10. Klasse:
(Mentor Verlag)
Winkelfunktionen,
Trigonometrie, Additionstheoreme, Vektorrechnung. |
Winkelfunktionen,
Trigonometrie, Additionstheoreme, Vektorrechnung. |
Mathe Lernhilfe
10. Klasse:
(Manz Verlag)
 |
| Algebra üben Gymnasium 10. Klasse |
Mathe Lernhilfe
10. Klasse:
(Manz Verlag)
 |
| Mathematik üben 10. Schuljahr |
Mathe Lernhilfe
10. Klasse:
(Stark Verlag)
 |
| Algebra 10. Klasse |
Mathe Lernhilfe
10. Klasse:
(Duden Verlag)
Logarithmen und Exponentialgleichungen
9./10. Schuljahr |
Mathe Lernhilfe
10. Klasse:
(Mentor Verlag)
| Exponential-und Logarithmen- gleichungen, Stochastik 10. Schuljahr |
Mathe Lernhilfe
10. Klasse:
(Mentor Verlag)
 |
| Gleichungen, Ungleichungen, Umkehrfunktionen, Potenzfunktionen 10. Schuljahr |
Mathe Lernhilfe
10. Klasse:
(Cornelsen Verlag)
 |
| Besser in Mathematik 10. Schuljahr |
Zentrische Streckung |
|
|||
Wie führe ich eine zentrische Streckung
durch?? (Thema der 9. Klasse) |
||||
Merke:
Die zentrische Streckung mit dem Streckfaktor k hat folgende
Eigenschaften:
| -
Das Bild einer Geraden ist wieder eine Gerade - Eine Gerade und ihre Bildgerade sind parallel, deshalb ist die Abbildung auch winkeltreu. - Jede Bildstrecke ist (deshalb hat auch jede Bildfigur den der Originalfigur. Ist k>0, so haben die Halbgeraden ZP und ZP´dieselbe Richung. bei k<0 haben ZP und ZP´eine entgegengesetzte Richtung. Das Streckzentrum Z ist stets FIXPUNKT !!! |
AUFGABE
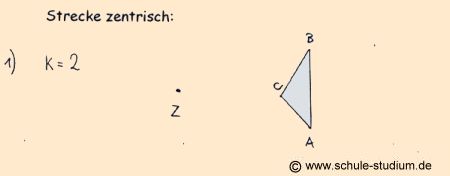
1)
Die zentrische Streckung bei einem Streckungsfaktor
von 2, wenn das Zentrum der
zentrischen Streckung Z außerhalb,
d.h. links vom Ausgangsdreieck liegt.
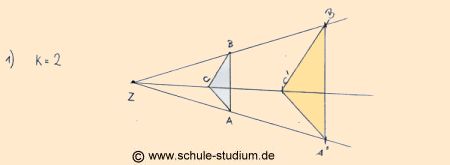
Vorgehensweise: Wir
verbinden Z mit jedem der drei Punkte des ursprünglichen Dreiecks
und über diese Punkte hinaus. Die abgemessene Entfernung ![]() ,
,![]() ,
, ![]() wird jeweils verdoppelt.
wird jeweils verdoppelt.
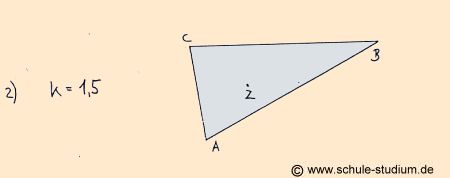
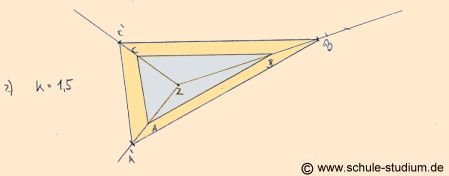
AUFGABE 2)
Die zentrische Streckung bei einem Streckungsfaktor
von 1,5, wenn das Zentrum der zentrischen Streckung im Inneren des
Dreiecks liegt.
Vorgehensweise: Wir
verbinden Z mit jedem der drei Punkte des ursprünglichen Dreiecks
und über diese Punkte hinaus. Die Entfernung ![]() ,
,![]() ,
, ![]() vergrößert
sich um den Faktor 1,5. Ungewohnt ist hier möglicherweise, dass das
ursprüngliche Dreieck ABC Teil des Bilddreiecks A´B´C´ist.
vergrößert
sich um den Faktor 1,5. Ungewohnt ist hier möglicherweise, dass das
ursprüngliche Dreieck ABC Teil des Bilddreiecks A´B´C´ist.
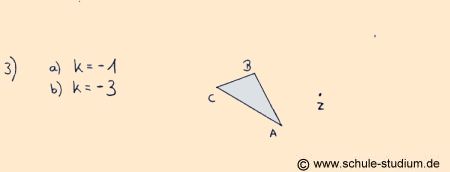
AUFGABE 3)
Die zentrische Streckung bei einem negativen Streckungsfaktor
von -1 bzw. -3, wenn das Zentrum der zentrischen Streckung rechts
vom Ausgangsdreiecks liegt.
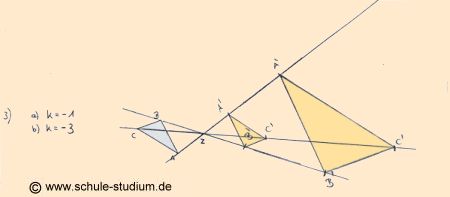
Vorgehensweise: Wir
verbinden wieder jeden der drei Punkte des Dreiecks mit dem Streckzentrum
Z
und über dieses hinaus.
Die Entfernung ![]() ,
,![]() ,
, ![]() bleibt
im ersten Fall(Aufgabe 3a) unverändert. Bei Aufgabe 3b)
vergrößert
sich das ursprüngliche Dreieck um den Faktor 3. Da der
Streckfaktor negativ ist, liegen Ursprungsdreieck und Bilddreieck
auf gegenüberliegenden Seiten.
bleibt
im ersten Fall(Aufgabe 3a) unverändert. Bei Aufgabe 3b)
vergrößert
sich das ursprüngliche Dreieck um den Faktor 3. Da der
Streckfaktor negativ ist, liegen Ursprungsdreieck und Bilddreieck
auf gegenüberliegenden Seiten.
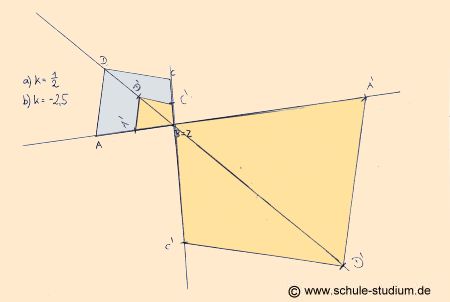
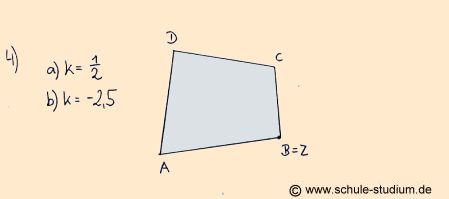
AUFGABE 4)
Die zentrische Streckung bei einem Streckungsfaktor
0<X<1 bzw. einem negativen Streckfaktor von -2,5, wenn
das Zentrum der zentrischen Streckung identisch mit einem Punkt
der
Figur ist.
(hier B=Z)
Vorgehensweise: B
ist in diesem Fall ein Fixpunkt.
Wir verbinden jeden der drei
Punkte des ursprünglichen Dreiecks mit dem Streckzentrum Z und über
dieses hinaus. Die abgemessene Entfernung ![]() ,
,![]() ,
, ![]() halbiert
sich im ersten Fall(Aufgabe 4a).
halbiert
sich im ersten Fall(Aufgabe 4a).
Bei Aufgabe
4b) vergrößert
sich das ursprüngliche Dreieck um den Faktor 2,5.
Ursprungsdreieck und Bilddreieck liegen auf gegenüberliegenden
Seiten von Z aus gesehen.