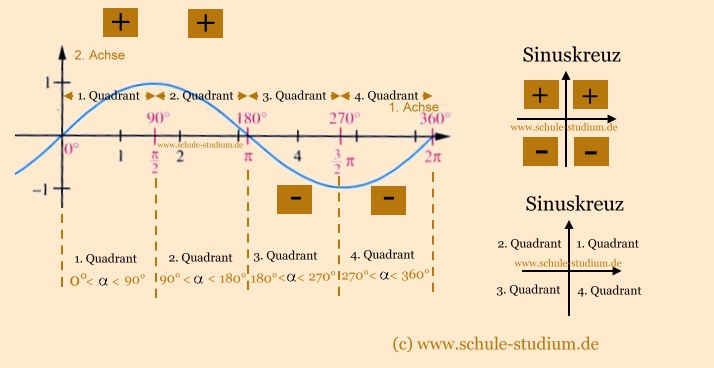
In der Mathematik werden 4 Quadranten unterschieden:

1. Quadrant 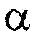: 0 < < 90°
2. Quadrant: 9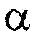0° < < 180°
3. Quadrant: 18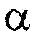0° < < 270°
4. Quadrant: 27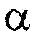0° < < 360°

An der Sinuskurve lässt sich schnell erkennen, dass Sinus im 1. und im 2. Quadranten positiv und
im dritten und vierten Quadranten negativ ist.


Weiterhin gilt:
I ) sin ( 180° - 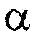) = sin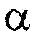
II) sin ( 180° + 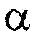) = - sin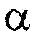
III) sin (360° - 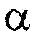=) = - sin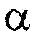


In unserem Koordinatensystem veranschaulicht:



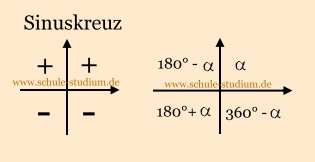
Was heißt das aber nun ?
Was kann ich damit anfangen?

Beispielaufgaben:

1) Drücke durch sin mit einem Winkel zwischen 0° und 90° aus !!

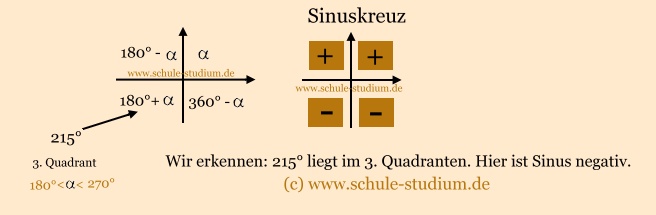
sin 215°

Wir suchen also einen Winkel 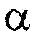zwischen 0° und 90°, der denselben Wert annimmt wie sin 215°.

Lösung:



Wir rechnen:

sin 215°

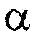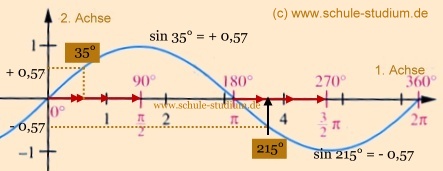
= sin ( 180° + ) = sin ( 180° + 35°) Da Sinus im 3. Quadranten jedoch negativ ist, muss gelten: sin 215° = - sin 35° Dies soll an der Sinuskurve veranschaulicht werden: sin 35° = + 0,57 sin 215° = - 0,57 Insofern muss gelten: sin 215° = - sin 35° - 0,57 = - (+0,57) Wir erinnern uns an das bereits zurückliegende Kapitel der Mathematik "Rechnen mit rationalen Zahlen" :  (  ) =

2) Drücke durch sin mit einem Winkel zwischen 0° und 90° aus !!

sin 165°

Wir suchen also einen Winkel 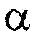zwischen 0° und 90°, der denselben Wert annimmt wie sin 165°.

Lösung:



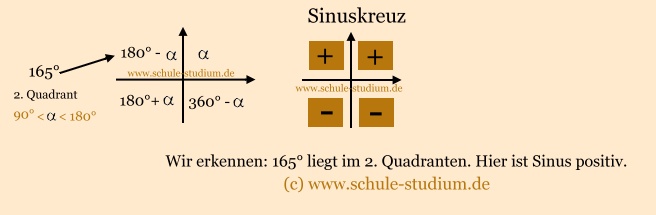
Wir rechnen:

sin 165°

= sin ( 180° - 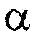) = sin ( 180° - 15°) Folglich gilt: sin 165° = + sin 15° oder einfach: sin 165° = sin 15° Auch diesmal veranschaulichen wir den Sachverhalt an der Sinuskurve:

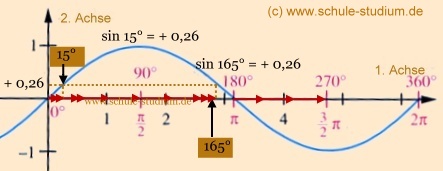
3) Drücke durch sin mit einem Winkel zwischen 0° und 90° aus !!

sin 300°

Wir suchen also einen Winkel 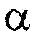zwischen 0° und 90°, der denselben Wert annimmt wie sin 300°.

Lösung:



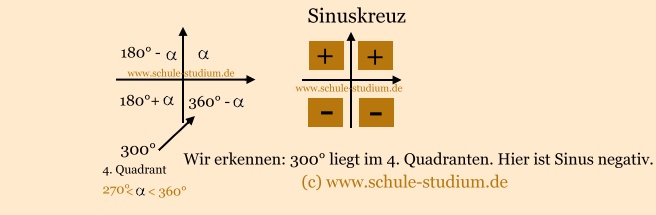
Wir rechnen:

sin 300°

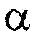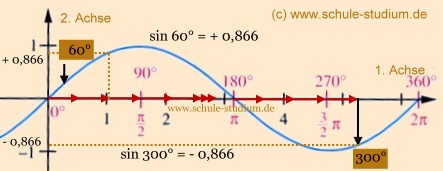
= sin ( 360° - ) = sin ( 360° - 60°) Da Sinus im 4. Quadranten jedoch negativ ist, muss gelten: sin 300° = - sin 60° Dies soll an der Sinuskurve veranschaulicht werden: sin 300° = - 0,866 sin 60° = + 0,866 Insofern muss gelten: sin 300° = - sin 60° - 0,866 = - (+0,866) Wir erinnern uns an das bereits zurückliegende Kapitel der Mathematik "Rechnen mit rationalen Zahlen" :  (  ) =

-> Sinus im Einheitskreis. Hintergrundwissen
-> Kosinus im Einheitskreis. Grundlagen und Übungen
-> Sinus- und Kosinusfunktionen. Grundlagen und Übungen